Root finding

Our purpose in this section will be to solve equations numerically, using Newton’s method

Functions in octave

Imagine that you are going to work a lot with a given function, $f(x)$, and you don’t want to type it continuously. You can define it for octave in this way:

> function y=f(x)
> y=exp(x)-x;
> endfunction

Now you can call it from the command line, it has become a function of octave:

> f(1)
ans = 1.7183

The name of the function is f, x is the argument, and y is the value where you should put the output. Of course, functions can have any name you want, and they can also take more than one argument, or can even take vectors as arguments.

Numerical Derivatives

Derivation is a straightforward, but boring task. Imagine that you want to plot a function $f(x)=\sin(\exp(x))$ along with its derivative, $f’(x)$, but you don’t want to take the effort to compute it. Let us do the following: put $f(x)$ in an octave function.

> function y=f(x)
> y=sin(exp(x));
> endfunction

Then, in order to get an approximate value of the derivative around, say, $x=1$, do the following:

> h=0.0001;
> x=1;
> (f(x+h)-f(x))/h
ans = -2.4786

Yes, we know that this formula only returns the derivative when the limit is taken and $h$ goes to zero. But, still, we can get a good approximation. In this case, we get -2.4786, while the real value of the derivative at that point is -2.4783. Fair enough.

We can use another function:

> function d=df(x)
> h=0.0001;
> d=(f(x+h)-f(x))/h;
> endfunction

This function needs f to be defined in order to work! So, if you have a well defined f, df is a well defined approximation to the derivative. Now, in order to plot them, we follow the standard procedure:

> x1=0:0.001:3.0;
> y1=f(x);
> y2=df(x);
> plot(x1,y1,x1,y2);

Nice, you will see this picture

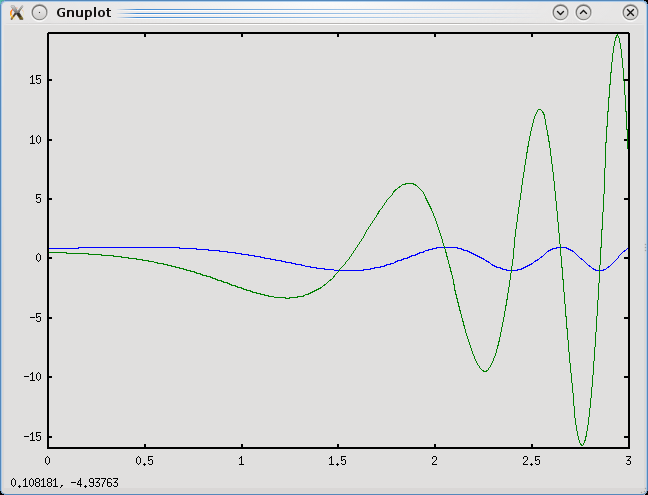
The blue line is the function, the green one the derivative. You can check easily that the maxima and minima of the function coincide with the zeroes of the derivative, as it should.

Script Files

There are functions that you don’t want to type again and again in octave. So what we can do is to create a script file. This is done outside. Open any text editor (please, plain text!! No word documents!!) and type the two functions we have used before, f and df. Comment lines just should start with # (and it is a good idea to include comment lines). So, this can be an example:

# Script file that computes a function and its derivative 
1; # This is included for technical reasons

# Function f(x) is defined here
function y=f(x)
y=sin(exp(x));
endfunction

# Now, the derivative function df/dx
function d=df(x)
h=0.0001; # Caution! You may want to change this value.
d=(f(x+h)-f(x))/h;
endfunction

This file has to be saved with a name ending in .m. For example: "functions.m". Now, enter octave and type

> source("functions.m")
> df(1)

And you will get the correct result.

Newton’s method

After a lot of previous work, we come to our original purpose, which is to solve any equation of the type $f(x)=0$ with Newton’s method. Consider the function we have used so far, $f(x)=\sin(\exp(x))$. From the plot, we can roughly see solutions to the equation. For example, there should be a solution near $x_0=1$. This is called an estimate.

Newton’s method gives us a way to improve the estimates in a very fast way. We approximate the function by its tangent line, as it can be seen in the next figure (courtesy of Wikipedia).

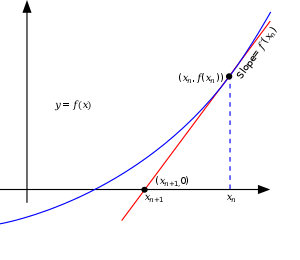
At the point $x=x_0$, The tangent line is given by the equation

And we solve the equation: $y=0$, i.e.: we find where does the tangent line cut the axis. This gives:

And this value is our next value of the estimate, which we shall call $x_1$. Of course, we repeat this argument over and over again, until the value does not change. Just a few iterations are needed. Then, we have a root of our function.

Our iteration can be written in this way:

This provides us with a rule to get $x_{n+1}$, i.e.: our next estimate, from $x_n$, i.e.: the previous one.

Let us see how it works in practice. Starting with $x=1$, we apply the rule and get:

> x=1;
> x-f(x)/df(x)
ans = 1.1675

And we get 1.1657 as our next estimate. We would like to work faster than that, so we may just say:

> x=1;
> for n=1:20
> x=x-f(x)/df(x)
> endfor

If we ask now for $x$ (just type x in octave), you get 1.1447. If you ask for $f(x)$, you get 1.224e-16 (in my machine, in yours it may change), which is close enough to zero for me. You may want to type format long in order to get many more digits and see that they are all converged.

Exercises

• Write a function that, when invoked, returns always the gaussian, $\exp(-x^2)$.

• Consider a quadratic equation, $ax^2+bx+c=0$. Write a function that takes $a$, $b$ and $c$ as arguments and returns one of the solutions.

• Write a newton function which takes an estimate and returns the value after (say) 20 iterations of Newton’s method.

• Solve the following equations with Newton’s method and check your results!

(a) $x^2=3$

(b) $\sin(x)=1/2-x$

(c) $\sin(\exp(x))=1/3$

• If you try to solve the equation $1-x^2=0$ and start out with $x_0=0$ you get into trouble. Why? How to get out of it?